1サイクルの中に何個のパターンがあるか
H27年度の洛北高校附属中学校「適性を見る検査Ⅲ」の問題をプログラミングで再現。
前回に続き、問2をみていきましょう。
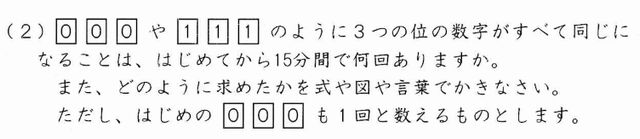
すべて同じ数がそろうのは、何パターンあるでしょうか。
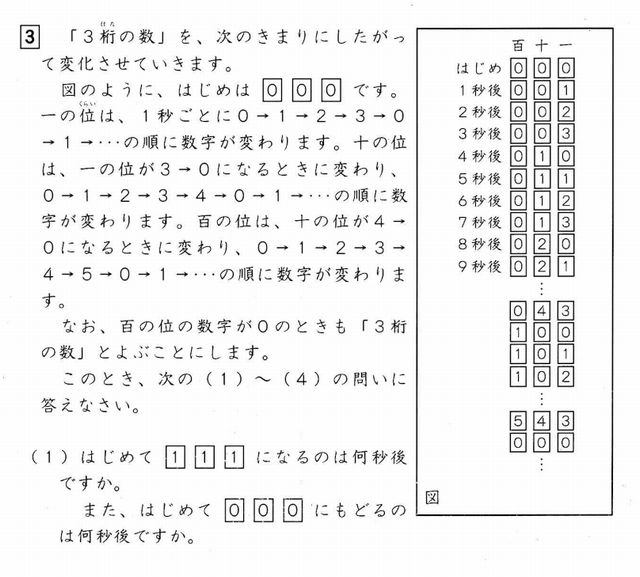
「000」…0秒
「111」…25秒
「222」…50秒
「333」…75秒
の4パターンがあります。
計算方法は次のとおりですね。
(20秒×百の位)+(4秒×十の位)+(1秒×一の位)
問1のように、再び「000」に戻るのは120秒のとき。
すなわち、120秒で1サイクルのプログラムです。
カウントのプログラムをつくる
問2をスクラッチで作ってみました。
3つの数字がそろれば、ネコが「そろった!」と言い、1カウント増える。

プログラムの中身はこのように。
スクラッチでは秒数でプログラムを動かすとき、どうしてもコンマ数秒のズレが出るので、今回は先頭に0.2秒を置いてます。

1秒間に変数が進みすぎないように考えたり、簡単に見えていろいろと工夫が必要なんですね。
1秒間に「1」だけ進む変数を作るのは、スクラッチではなかなか大変なのです。
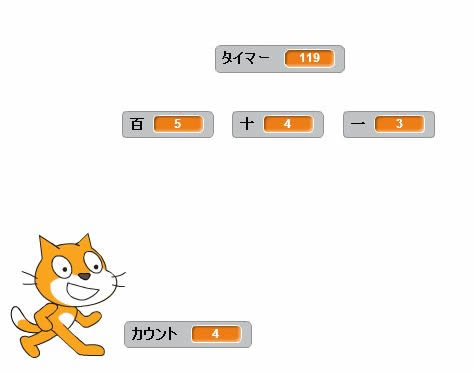
119秒時点でのカウント数は「4」になってますね。
3つの数字がそろうのは、1サイクルで4回あることが確認できました。
15分=900秒なので、900秒÷120秒=7.5サイクル
7サイクル×4回=28回
ですが、0.5サイクルは?
120秒×0.5=60秒
60秒時点で何回そろうのかを数えないといけません。
○「000」…0秒
○「111」…25秒
○「222」…50秒
✖「333」…75秒
はい、3回ですね。
なので正解は28+3=31回ということになります。







