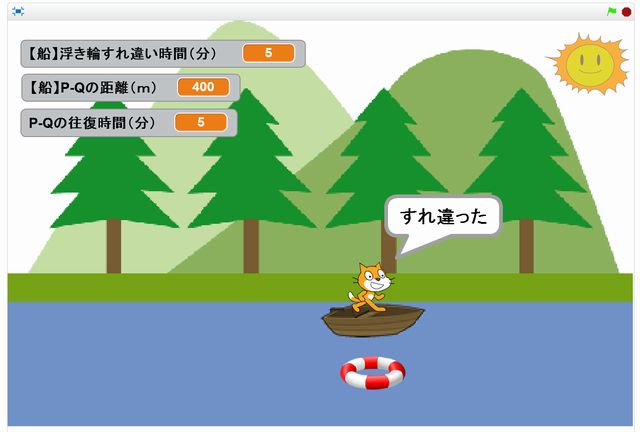
スクラッチ向けに単位を合わせよう
今回は大阪の高槻中学校、平成27年度中期の算数、問1(4)をスクラッチで再現したいと思います。

この文章題をスクラッチで再現しようと思うと、まず迷うのが「単位をどうしようか…」ということじゃないでしょうか。㎞だったり時速だったり少数も出てきたりで、頭を悩ませてしまいます。おまけに、「5分後」まで待ってられない…。
スクラッチの横幅は480歩(ピクセル)、縦は360歩(ピクセル)です。距離(㎞)は、このピクセルで表わせるように考えましょう。
距離をピクセルに、分速を秒速に
ということで、スクラッチ式に文章題を変えてみました。
・5分後→5秒後
・船の静水 毎時6キロ … 分速100m → 10歩/秒
・川の流れ 毎時1.2キロ … 分速20m → 2歩/秒
これを踏まえて、スクラッチ向けに問題文を変えてみると以下のように。

スタート位置とトータル秒数
船のスピードは静水の時ということで、船の上りと下りの速さは違ってきます。
船の速度
・上流…8歩/秒(10歩-2歩)
・下流…12歩/秒(10歩+2歩)
上りは遅くて下りは速いんですね。こういう川を題材にした問題は、中学受験でよく出題されます。
では、解きやすいところから手を付けていきましょう。まずはP地点から5秒後の地点を「R」と名付けることにします。
P地点~R地点の距離がわかります。
8歩×5秒=40歩
これを船のスプライトで再現すると…
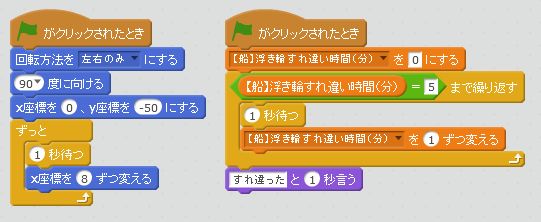
スタートのX座標は0にしています。
そして「浮き輪すれ違い時間」という変数をつくり、すれ違ったときに「すれ違った!」というようにしました。

これがわかると、船がP地点からQ地点で折り返し、P地点にゴールするまでの時間がわかるように。
今度は浮き輪を動かして、その時間を計ってみましょう。
プログラムはこんな風に組んでみました。
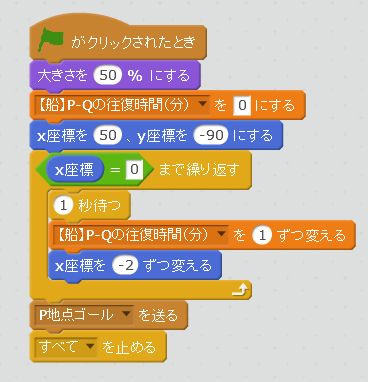
ここでは、浮き輪のスタート位置はX座標50にします。というのも、5秒後に船とすれ違うのはX座標が40のとき。X座標50からスタートすれば、ちょうど船とすれ違うんですね。
そして、X座標0になるまで繰り返すと。
さっそく、動かしてみましょう。
船のスプライトは一旦隠しておきます。
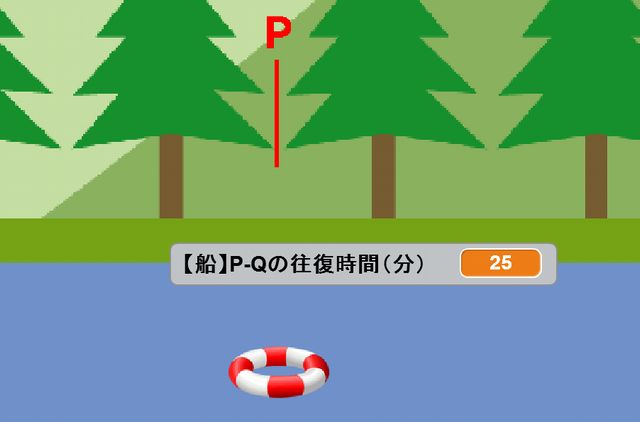
25秒と出ました。
考えてみると、浮き輪がR地点からP地点にゴールする時間は、40歩÷2歩=20秒。
これに5秒足した時間は、船のP地点→Q地点→P地点のトータル時間と同じですね。
これをもとに、上りと下りでそれぞれにかかった時間(秒数)を求めます。
続きは次回ゼミノートで。
実際の動きはこちら。
(※iPhoneなどのスマホからはFlashが動作しません。なるべくPCから閲覧ください。)






